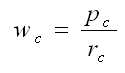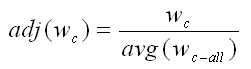Weighting

An Explanation of Weighting in NSSE Reports

A graphical icon of a scale. Source: Icon created by Freepik - Flaticon (www.flaticon.com).

What is weighting?

Weighting is the process of adjusting data to reflect differences in the number of population units that each respondent represents. For example, if the proportion of men in a student population is 50%, but the proportion of men who respond is only 33%, then we assign a higher weight to respondents who are men so that the results more accurately reflect the proportions of genders within the student population. In practical terms, a weight is a number in a data file assigned to each respondent, and is used as a multiplier to adjust the number of cases used in a calculation.

Why does NSSE weight?

Weighting is necessary when two conditions are present: (a) The proportion of respondents within a particular demographic variable (e.g., gender identity, race/ethnicity, or age) differs substantially from their population percentages, and (b) students within the subgroups differ substantially in the variables of interest (e.g., students of different genders show different patterns of engagement).

Analysis of these conditions compels NSSE to weight by gender, enrollment status, and institutional size. Men and part-time students consistently have lower response rates than women and full-time students. From the literature and past NSSE results we know that students of different genders have different engagement patterns, and part-time students differ to a great extent from full-timers.

In terms of institutional size, we know that the numbers of students attending institutions within comparison groups are disproportionate to their actual population sizes. This is caused mostly by varying response rates between institutions. NSSE has also consistently observed that enrollment size is related to engagement levels.

How NSSE computes weights

For each institution, sets of weights are computed separately for first-year and senior students using gender and enrollment status information taken from submitted population files. Since multiple categories exist for each key background characteristic, NSSE calculates specific weights for multiple types of students: (1) full-time men, (2) full-time women, etc. We refer to each of these categories as “cells.”

The first step in NSSE’s weight calculation is represented by the following formula where pc equals the overall population size and rc equals the number of respondents for any given cell.

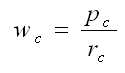
This initial weight calculation serves two purposes: (a) It corrects for any disproportionate representation within cells, and (b) it adjusts the number of respondents to original population counts during statistical calculations. Institutional data files delivered each summer include the results of this calculation under the variable WEIGHT2.

The second and final step of NSSE’s weight calculation is represented by the following formula where avg(wc-all) equals the average of WEIGHT2 for all respondents across all four cells at a particular institution whose reports are being developed.

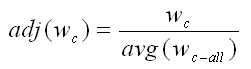
When developing an individual school’s reports, we recognize that the value for avg(wc-all) used to divide WEIGHT2 values does not vary by institution. In essence, we divide by this constant to preserve the original respondent count for any given institution for which reports are being created, but also to ensure proportional representation of institutions within selected peer groups. In summary, when looking at reports, readers should understand that the weighted count for the institution equals the number of respondents and that the weighted count for comparison groups reflects proportional representation, but is an arbitrary respondent count.

In an institution's data file, WEIGHT1 contains the respondent weights as described above for the institution. Thus, institution analysts who want to reproduce their report numbers should use WEIGHT1. Using WEIGHT1 or WEIGHT2 will lead to essentially the same frequencies and means, but the counts upon which these results are based will differ (i.e., respondent versus population).

Advantages to this weighting approach

To summarize, this weighting approach has a few advantages. The weights ensure that comparison groups will not be disproportionately represented by any given institutional member, regardless of their sampling approach and response rate. Furthermore, the original respondent count is preserved for the institution whose report is being created. Lastly, NSSE continues to weight all standard reports to promote transparency, consistency of interpretation, and result validity.

Caution about using weights for within-institution analyses

Using NSSE weights is generally not appropriate for intra-institutional comparisons, such as analyzing engagement results by Honors College participation status. Weights included in institutional data files are designed to give the best estimate of the entire institution, not any particular campus sub-group. We encourage schools interested in looking more closely at their data to use a more sophisticated or locally-derived weighting approach that would address any disproportionate representation and engagement result variation by different student types.

References

Chen, P. D., & Sarraf, S. (2007, June 4). Creating weights to improve survey population estimates. Workshop presented at the 47th Annual Forum of the Association for Institutional Research, Kansas City, MO.

Cohen, B. H. (2001). Explaining psychological statistics (2nd ed.). New York: John Wiley & Sons.

Höfler, M., Pfister, H., Lieb, R., & Wittchen, H. (2005). The use of weights to account for non-response and drop-out. Social Psychiatry and Psychiatric Epidemiology, 40, 291-299.

Little, R. J. A. (1993) Post-Stratification: A Modeler's Perspective. Journal of the American Statistical Association, 88, 1001-1012.